I. Các Công Thức Lượng Giác sin cos tan cot Lớp 9 10 11 và Bài Tập
1. Khái niệm tỉ số lượng giác của một góc nhọn
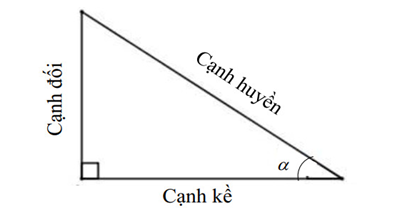
Với:
sin : là tỉ số giữa cạnh đối và cạnh huyền của góc
cos : là tỉ số giữa cạnh kề và cạnh huyền của góc
tan : là tỉ số giữa cạnh đối và cạnh kề của góc
cot : là tỉ số giữa cạnh kề và cạnh đối của góc
Mẹo học thuộc : Sin đi học, Cos không hư, Tan đoàn kết, ,Cot kết đoàn
Xem thêm :
- Công thức tính thể tích khối tứ diện
- Cách tính phần trăm giảm giá? [Cập nhập 2023]
- Cơ năng là một đại lượng
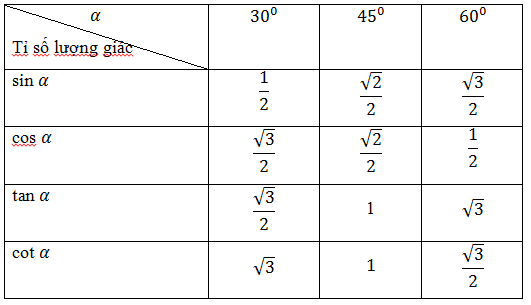
2. Bảng tỉ sô lượng giác lớp 9 của một số góc đặc biệt.
a, Tỉ số lượng giác của 2 góc phụ nhau. ( α + β = 90° )
sin α = cos β cos α = sin β
tan α = cot β cot α = tan β
b, Bảng tỉ số của các góc đặc biệt.
3. Bài tập vận dụng các công thức lượng giác sin cos
a, Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
Giải :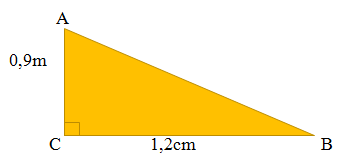 
– Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:
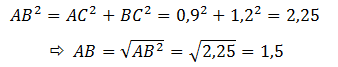
– Các tỉ số lượng giác của góc B là :
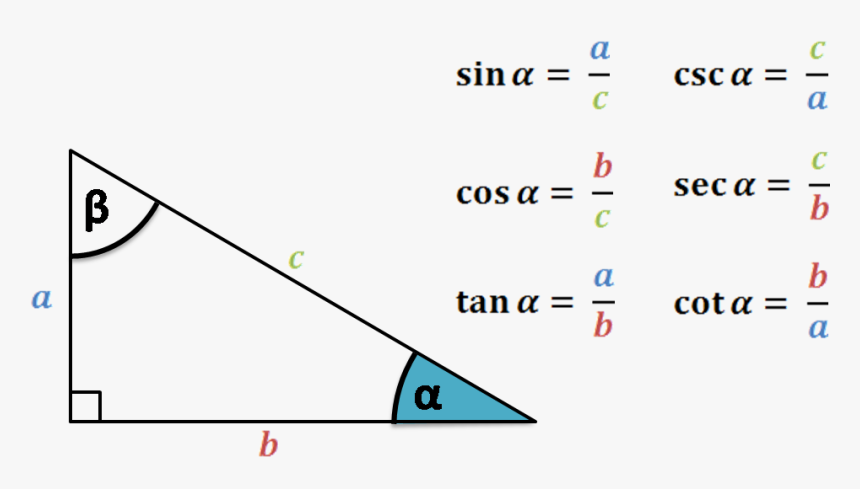
II. Bảng Các Công Thức Lượng Giác Lớp 10 11 và Bài Tập
Bước sang cấp 3, lượng giác không chỉ dừng lại ở các công thức cơ bản như trên, mà nó đã vươn lên một “đẳng cấp” và “tầm cao” mới, cùng với đó là vai trò “kiếm điểm” cho các bạn sĩ tử. Sau đây là phần tổng quan kiến thức lượng giác, hi vọng sẽ giúp đỡ các bạn phần nào trong việc ghi nhớ và ôn tập kiến thức một cách tốt nhất. Việc ghi nhớ công thức lượng giác cũng như việc nhớ 7 hằng đẳng thức đáng nhớ khi các em học lớp 8, 9.
1. Bảng tỉ số lượng giác lớp 10
1.1 Các hằng đẳng thức lượng giác cơ bản.
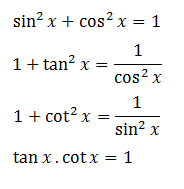
1.2. Các cung có liên quan đặc biệt.
a, Cung đối nhau:
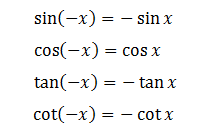
b, Cung bù nhau: x và π-x
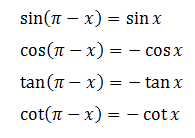c, Cung phụ nhau: x và π⁄2 – x
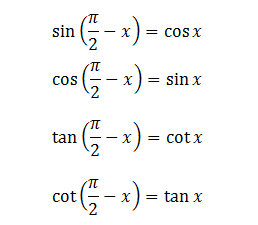d, Cung hơn kém nhau π : χ và π + χ
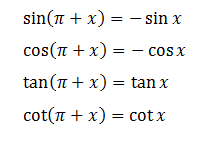
e, Cung hơn kém nhau π⁄2 : χ và χ + π⁄2
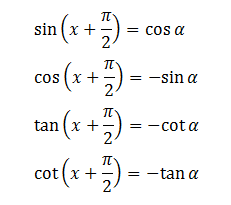
1.3. Công Thức Cộng.
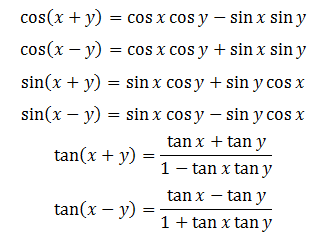
1.4. Công Thức Nhân Đôi.
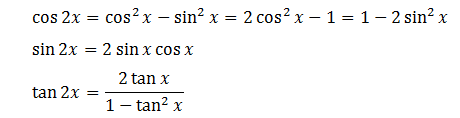
1.5. Công Thức Hạ Bậc.
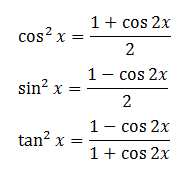
1.6. Công Thức Tính sin x, cos x, tan x theo t=tan x/2
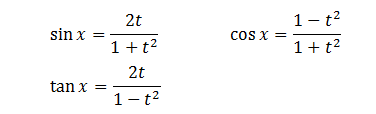
1.7. Công Thức Nhân Ba.
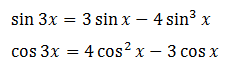
1.8. Công Thức Biến Đổi Tổng Thành Tích.
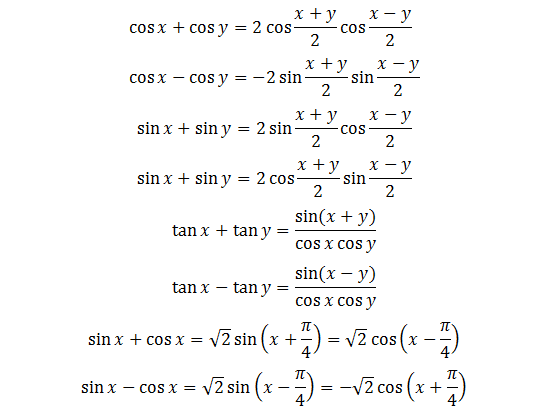
1.9. Biến Đổi Tích Thành Tổng.
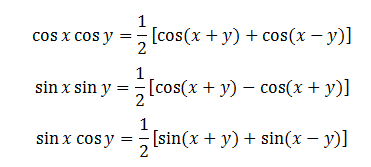
III. Một Số Kĩ Năng Cơ Bản Để Giải Phương Trình Lượng Giác
1. Giải phương trình lượng giác bằng cách đưa về phương trình tích.
a. Lưu ý :
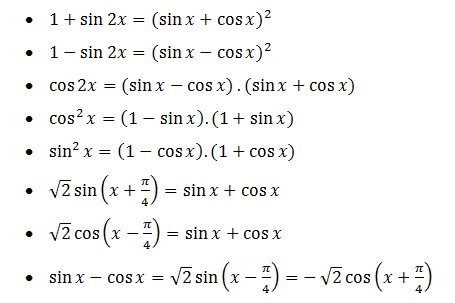b. Ví dụ.
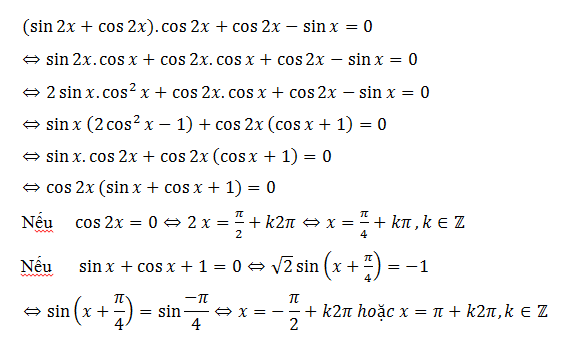
2. Giải phương trình bằng cách đưa về phương trình bậc cao đối với 1 hàm số lượng giác.
a. Lưu ý:
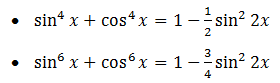b. Ví dụ:
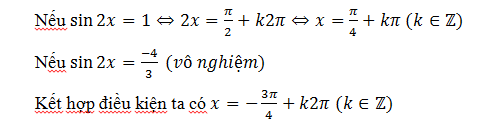
3. Giải phương trình bằng cách đưa về dạng asinx+bcosx
a. Dấu hiệu :
Xuất hiện √3 rồi đưa về dạng trên theo cos hoặc sin đứng sau √3
b. Ví dụ :
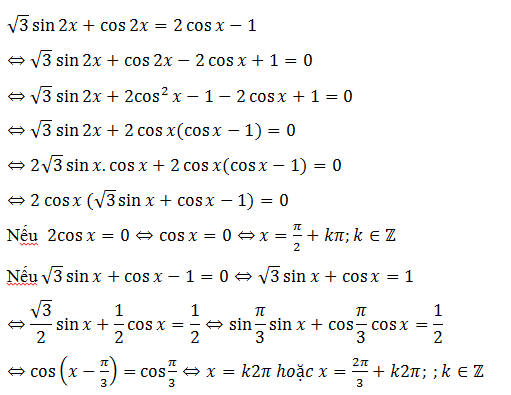
IV. Mọi người cũng hỏi
Sin và cos là gì trong toán học?
Trả lời: Sin và cos là hai hàm số lượng giác cơ bản trong toán học. Sin (sin) thể hiện tỉ lệ giữa độ dài cạnh đối diện và độ dài đường kính trong tam giác vuông. Cos (cos) thể hiện tỉ lệ giữa độ dài cạnh kề và độ dài đường kính.
Sin và cos có ứng dụng trong những lĩnh vực nào?
Trả lời: Sin và cos được áp dụng rộng rãi trong toán học, vật lý, kỹ thuật, thống kê, và nhiều lĩnh vực khoa học khác. Chúng giúp mô tả và tính toán sự biến đổi chu kỳ, dao động, và các mối liên hệ góc trong các hệ thống.
Cách tính giá trị của sin và cos trong tam giác vuông?
Trả lời: Để tính giá trị sin và cos trong tam giác vuông, cần biết góc và độ dài các cạnh liên quan. Sin (sin) của góc bằng độ dài cạnh đối diện chia cho độ dài đường kính; cos (cos) của góc bằng độ dài cạnh kề chia cho độ dài đường kính.
Sin và cos có tính chất đặc biệt nào?
Trả lời: Một số tính chất của sin và cos bao gồm chu kỳ, đối xứng, và mối quan hệ với nhau:
sin
